Функции для решения нелинейных уравнений и систем
Функция поиска корня нелинейного уравнения root
Многие уравнения, например трансцендентные, и системы из них не имеют аналитических решений. Однако они могут решаться численными методами с )аданной погрешностью (не более значения, заданного системной переменной TOL).
Для простейших уравнений вида F(x)=0 решение находится с помощью функции
гооt (Выражение, Имя_переменной)
Эта функция возвращает значение переменной с указанным уровнем, при котором выражение дает 0. Функция реализует вычисления итерационным методом, причем можно задать начальное значение переменной. Это особенно полезно, если возможно несколько решений. Тогда выбор решения определяется выбором начального значения переменной. Рис. 11.30 иллюстрирует технику применения функции root
для вычисления корней кубического полинома.
Рис. 11.30 Вычисление корней кубического полинома

Как известно, кубическое уравнение обязательно имеет хотя бы один кубический корень х1. Он найден вначале функцией root. Два других корня могут оказаться и комплексными. Функция root может отыскивать и такие корни. Для поиска второго корня, х2,
первый исключается делением F(x) на (х-х1).
Соответственно для поиска третьего корня, х3, F(X)
делится еще и на (х-х2). Эту процедуру можно распространить и на поиск корней полиномов более высокой степени, однако надо помнить, что найти корни полинома можно гораздо более изящным и простым способом — используя операцию символьных вычислений.
Функция поиска корней многочлена polyroots
Для поиска корней обычного полинома р(х) степени п MathCAD содержит очень удобную функцию:
polyroots(V)
Она возвращает вектор корней многочлена (полинома) степени п,
коэффициенты которого находятся в векторе V, имеющем длину равную п+1.
Заметим, что корни полинома могут быть как вещественными, так и комплексными числами. Не рекомендуется пользоваться этой функцией, если степень полинома выше пятой-шестой, так как тогда трудно получить малую погрешность вычисления корней. На рис. 11.30 в конце документа приведен пример вычисления корней кубического полинома с применением функции polyroots.
Функция root в составе функции пользователя
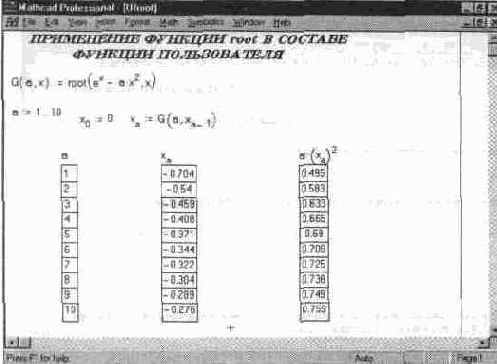
Функцию root можно использовать и в составе функций пользователя, что нередко позволяет получать довольно простые решения для нетривиальных задач. Примером может служить вычисление неполной гамма-функции G(a,x), показанное на рис. 11.31.
Рис. 11.31 Вычисление функции G(a,x) с помощью функции root в составе функции пользователя
Директива Given для подготовки блока решения системы уравнений
При решении систем нелинейных уравнений используется специальный вычислительный блок, открываемый служебным словом — директивой Given — и имеющий следующую структуру:
Given
Уравнения
Ограничительные условия Выражения с функциями find и minerr
Рекомендуется дополнить блок проверкой решения системы.
Функции find и minerr для решения систем нелинейных уравнений
В блоке используется одна из следующих двух функций:
find(vl, v2, ..., vn) — возвращает значение одной или ряда переменных
для точного решения;
minerr(vl, v2, ..., vn) — возвращает значение одной или ряда переменных
для приближенного решения. Между этими функциями существуют принципиальные различия. Первая функция используется, когда решение реально существует (хотя и не является аналитическим). Вторая функция пытается найти максимальное приближение даже к несуществующему решению путем минимизации среднеквадратичной погрешности решения.
Ввод ограничений при решении систем нелинейных уравнений
Ограничительные условия задаются обычно с помощью операторов — знаков отношения величин. Особо следует отметить знак приближенного равенства (в версиях MathCAD под Windows это жирный знак равенства, тогда как в более ранних версиях под MS-DOS это был знак приближенного равенства), который используется для указания начального значения переменных при итерационных вычислениях.
Оператор Клавиши Значение оператора
е1>е2 е1>е2 е1 больше е2 е1 < е2 е1<е2 е1 меньше е2 е1 > е2 el Ctrl ) е2 е1 больше или равно е2 е1 < е2 Ctrl ( е2 е1 меньше или равно е2 е1у:е2 el Ctrl # е2 е1 не равно е2 el=e2 elCtrl=e2 el равно е2
Примеры решения нелинейных уравнений
Функции find и minerr могут использоваться для решения одного или ряда уравнений. Рис. 11.32 показывает решение некорректно поставленной задачи. Фактически решается система взаимно несовместимых уравнений x=i0 и х^З. Поэтому MathCAD реагирует на попытку решения сообщением об ошибке.
Рис. 11.32 Пример решения простой некорректной задачи

Более правомерной является постановка вопроса о приближенном решении уравнения х2 =3 при приближенном задании x=10 в качестве начального приближения к решению. При этом для записи уравнения используется особый (жирный) знак равенства. Как видно на рис. 11.32, здесь обе функции (find и minerr)
дают одинаковое решение.
Рис. 11.33 иллюстрирует решение другой задачи — поиск точек пересечения параболы отрезком прямой. В нашем случае с помощью функции Find решается система из двух уравнений (одно из них нелинейное) с ограничительными условиями, задающими область поиска корня (x<0 для отрицательного корня и х>0
для положительного).

Рис. 11.33 Вычисление координат точек пересечения параболы прямой
Еще один пример решения системы нелинейных уравнений (на этот раз с помощью функции minerr) показан на рис. 11.34.
Рис. 11.34 Решение системы из двух уравнений с помощью функции minerr

При использовании функции
minerr для решения систем нелинейных уравнений надо проявлять известную осторожность и обязательно предусматривать проверку решений. Нередки случаи, когда решения могут оказаться ошибочными, чаще всего из-за того, что из нескольких корней система предлагает нереальный (или не представляющий интереса) корень. Полезно как можно точнее указывать начальные приближения к решению.