Параметрическая трехмерная графика
При построении трехмерных поверхностей и объемных фигур можно использовать параметрическое задание описывающих их функций. Фигуры задаются значениями координат х, у и z всех точек фигуры. При этом в шаблоне 3D-графики указываются три матрицы, хранящие массивы этих координат, — X, Y и Z. Ниже представлены интересные примеры применения такой графики.
Построение сферы
На рис. 14. 1 показано построение в трехмерном пространстве сферы. Сфера строится из каркаса, причем число деления ее по вертикали N задается в начале построения. Затем вычисляются массивы опорных точек каркаса, которые представлены матрицами X, Y и Z.

Рис. 14. 1 Построение сферы
Используя различные форматы 3D-графиков, можно выполнить рисунок сферы в различных стилях, в том числе с цветной или черно-белой окраской. Однако в таком случае каркасное построение с применением алгоритма удаления невидимых линий дает, пожалуй, наиболее наглядное представление о характере этой простой объемной фигуры. На рис. 14. 1 представлено два варианта построения сферы с применением различной функциональной окраски.
Параметрическое задание трехмерной поверхности позволяет эффективно применять форматирование их графиков, в частности задавая углы обзора 3D-фигур и меняя их функциональную окраску. К тому же визуализацию таких фигур можно существенно улучшить.
Построение фигуры вращением линии вокруг оси Х
Интересные объемные фигуры можно получить, вращая некоторую кривую вокруг той или иной оси. При этом необходимо обеспечить пересчет координат всех узловых точек фигуры по известным из геометрии формулам. На рис. 14. 2 показано построение такой фигуры вращением линии, заданной функцией f (x),
вокруг оси X.
В документе на рис. 14. 2 приведены все необходимые формулы для пересчета координат узловых точек фигуры при ее вращении. Даны также графики исходной кривой (слева внизу) и фигуры, полученной ее вращением (справа внизу). Фигура напоминает опрокинутую рюмку, лежащую на плоскости. Она построена без применения функциональной окраски, но с использованием алгоритма удаления невидимых линий.
Построение фигуры вращением линии вокруг оси Y
Таким же способом можно построить фигуру, полученную вращением исходной кривой вокруг оси Y. Это демонстрирует документ, показанный на рис. 14. 3.
Чтобы показать возможности задания различного стиля рисунков, в нашем случае фигура построена с удалением невидимых линий каркаса и с при-
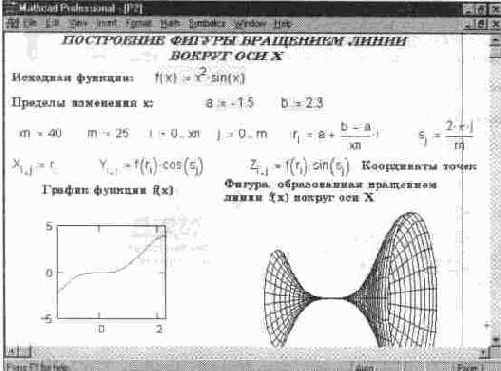
Рис. 14. 2 Построение фигуры вращением линии вокруг осиХ
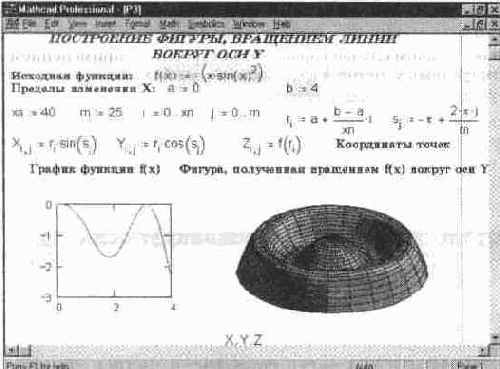
Рис. 14. 3 Построение фигуры вращением линии вокруг оси Y
менением функциональной окраски. Нетрудно заметить, что это делает фигуру очень наглядной.
Построение графика объемной спирали
3D Scatter Plot — вид трехмерных графиков, особенно удобный для представления пространственного расположения множества мелких объектов, условно называемых точками. На рис. 14. 4 показано применение этого графика для построения 100 точек, лежащих на пространственной спирали, напоминающей растянутую пружину.
Для каждой точки в этом случае необходимо располагать тремя координатами — X, Y и Z. Их совокупность образует три одноименных вектора. Вви-

Рис. 14. 4 Построение графика вида 3D Scatter Plot для точек пространственной спирали
ду простоты алгоритма построения необходимости в более подробном его описании нет. Заметим лишь, что число точек N
можно менять.
Построение пространственной фигуры — узлов, образованных толстыми "канатами"
О больших возможностях графики MathCAD PLUS 7. 0 PRO свидетельствует пример, приведенный на рис. 14. 5. Он же иллюстрирует применение типовых матричных функций для описания и пространственного преобразования сложной трехмерной фигуры — узлов, образованных толстыми "канатами".
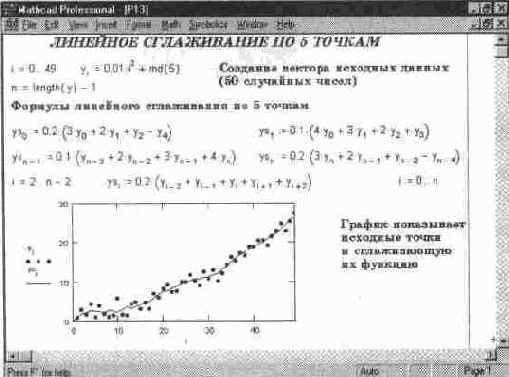
Рис. 14. 5 Построение фигуры — узлов, образованных толстыми "канатами" (начало документа)
Сама фигура, построенная по алгоритму, представленному на рис 145, изображена на рис 146

Рис. 14. 6 Вид фигуры (конец документа)
Изменяя параметр К,
можно получить множество других объемных фигур Функциональная окраска придает фигуре весьма реалистичный вид Этот пример наглядно показывает, что по возможностям графики система MathCAD 7 О PRO уже приближается к системе Mathematica 222, лидеру среди систем символьной математики для персональных компьютеров