Возможности символьного процессора (Symbolic)
Системы компьютерной алгебры снабжаются специальным процессором для выполнения аналитических (символьных) вычислений. Его основой является ядро, хранящее всю совокупность формул и формульных преобразований, с помощью которых производятся аналитические вычисления. Чем больше этих формул в ядре, тем надежней работа символьного процессора и тем вероятнее, что поставленная задача будет решена, разумеется, если такое решение существует в принципе (что бывает далеко не всегда).
Ядро символьного процессора системы MathCAD — несколько упрощенный вариант ядра известной системы символьной математики Maple V фирмы Waterloo Maple Software [12, 18], у которой MathSoft (разработчик MathCAD) приобрела лицензию на его применение, благодаря чему MathCAD стала (начиная с версии 3. 0) системой символьной математики.
Прямой доступ к большинству операций ядра (возможный в системе Maple V R3/R4), для пользователя MathCAD, к сожалению, закрыт. К примеру, библиотечный модуль Maple V содержит около 100 функций линейной алгебры, тогда как в модуле MathCAD 3. 0 есть только три важнейшие функции из этого раздела. Многие функции и правила преобразования в ядре используются лишь для получения промежуточных преобразований.
Тем не менее это обстоятельство нельзя считать уж слишком большим недостатком системы MathCAD. Во-первых, потому, что ее назначение иное — прежде всего решение задач в численном виде, а во-вторых, потому, что система Maple V явно избыточна (в ее ядре около 2800 функций и правил преобразования) и ориентирована на пользователей с весьма далекими от средних потребностями в решении задач компьютерной алгебры (символьной математики) [12].
Введение в систему MathCAD символьных вычислений придает ей качественно новые возможности, которые отсутствовали у прежних версий системы [5—7]. Теоретические сведения об алгоритмах компьютерной алгебры можно найти в книге [19]. Куда важней, что символьные вычисления выполняются в конечном счете столь же просто (для пользователя), как, скажем, вычисление квадрата х.
Операции, относящиеся к работе символьного процессора, содержатся в подменю позиции Symbolic (Символика) главного меню (см. рис. 8. 1).
Чтобы символьные операции выполнялись, процессору необходимо указать, над каким выражением эти операции должны производиться, т е надо выделить выражение (правила выделения неоднократно описывались выше) Для ряда операций следует не только указать выражение, к которому они относятся, но и наметить переменную, относительно которой выполняется та или иная символьная операция. Само выражение в таком случае не выделяется. ведь и так ясно, что если маркер ввода выделяет переменную какого-либо выражения, то это выражение уже отмечено наличием в нем выделяемой переменной
Рис. 8. 1 Вид экрана системы с подменю позиции Symbolic главного меню
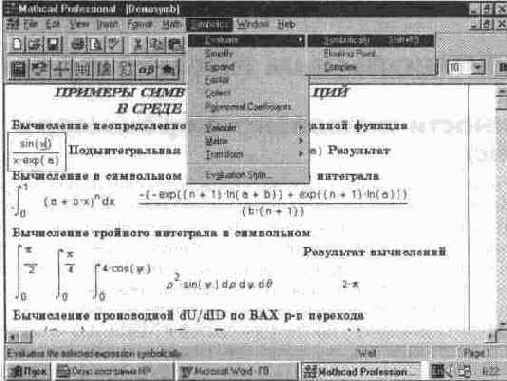
Символьные операции разбиты на пять характерных разделов Первыми идут наиболее часто используемые операции Они могут выполняться с выра жениями, содержащими комплексные числа или имеющими решения в комплексном виде
Операции с выделенными выражениями
К операциям с выделенными выражениями относятся следующие Evaluate
(Вычислить) — преобразовать выражение с выбором вида преоб разований из подменю,
Simplify (Упростить) — упростить выделенное выражение с выполнением таких операций, как сокращение подобных слагае мых, приведение к общему знаменателю, использова ние основных тригонометрических тождеств и т д, Expand
(Разложить — раскрыть выражение [например, для по степеням) (Х+ Y) (Х- Y) получаем X2- Y2}, Factor
(Разложить — разложить число или выражение на множи-на множители) тели [например X2-Y2 даст (X+ Y) (X-Y)], Collect
(Разложить — собрать слагаемые, подобные выделенному по подвыражению) выражению, которое может быть отдельной переменной или функцией со своим аргументом (ре зультатом будет выражение, полиномиальное от носительно выбранного выражения),
Polynomial Coefficients — найти коэффициенты полинома по заданной
(Полиномиальные переменной, приближающего выражение,
коэффициенты) в котором эта переменная использована
Операции с выделенными переменными
К числу операций с выделенными переменными относятся
Solve (Решить — найти значения выделенной переменной,
относительно переменной) при которых содержащее ее выражение становится равным нулю (решить уравнение или неравенство относительно выделенной переменной);
Substitute (Заменить — заменить указанную переменную содержи-
переменную) мым буфера обмена;
Differentiate —
дифференцировать все выражение, содержа- (Дифференцировать щее выделенную переменную, по отношению по переменной) к этой переменной (остальные переменные рассматриваются как константы);
Integrate (Интегрировать — интегрировать все выражение, содержащее
по переменной) выделенную переменную, по этой переменной;
Expand to Series... — найти несколько членов разложения выра- (Разложить в ряд) жения в ряд Тейлора относительно выделен ной переменной;
Convert to Partial Fraction — разложить на элементарные дроби выраже- (Разложить на элементарные ние, которое рассматривается как рацио-дроби) нальная дробь относительно выделенной пе ременной.
Операции с выделенными матрицами
Операции с выделенными матрицами представлены позицией подменю Matrix
(Матричные операции), которая имеет свое подменю со следующими операциями:
Transpose (Транспонировать) — получить транспонированную матрицу;
Invert (Обратить) — создать обратную матрицу;
Determinant
(Определитель) — вычислить детерминант (определитель) матрицы.
Операции преобразования
В MathCAD 7.
0 PRO в позиции Symbol
содержится раздел операций преобразования, создающий подменю со следующими возможностями:
Fourier Transform — выполнить прямое преобразование Фурье
(Преобразование Фурье) относительно выделенной переменной;
Inverse Fourier Transform — выполнить обратное преобразование
(Обратное преобразование Фурье относительно выделенной
Фурье) переменной;
Laplace Transform — выполнить прямое преобразование (Преобразование Лапласа) Лапласа относительно выделенной пере менной (результат — функция от пере менной s);
Inverse Laplace Transform — выполнить обратное преобразование (Обратное преобразование Лапласа относительно выделенной Лапласа) переменной (результат — функция от переменной t);
Z Transform
(Z-преобразование) — выполнить прямое Z-преобразование вы ражения относительно выделенной пере менной (результат — функция от пере менной z);
Inverse Z Transform — выполнить обратное Z-преобразование (Обратное Z-преобразование) относительно выделенной переменной (результат — функция от переменной n)
Стиль эволюции
К стилю эволюции относится одна операция-
Evaluation Style... — задать вывод результата символьной операции под
(Стиль эволюции) основным выражением, рядом с ним или вместо него
В последующих разделах этой главы каждая из упомянутых выше операций будет рассмотрена более подробно с необходимыми примерами.